A seguir, apresentamos a resolução detalhada da questão de função quadrática fornecida e, na sequência, sugestões de questões similares e relevantes para a sua plataforma de ensino a distância (LMS) em WordPress, focada em exatas.

1. Resolução Detalhada da Questão

Questão: Observando o gráfico abaixo, a função $f(x)$ é:

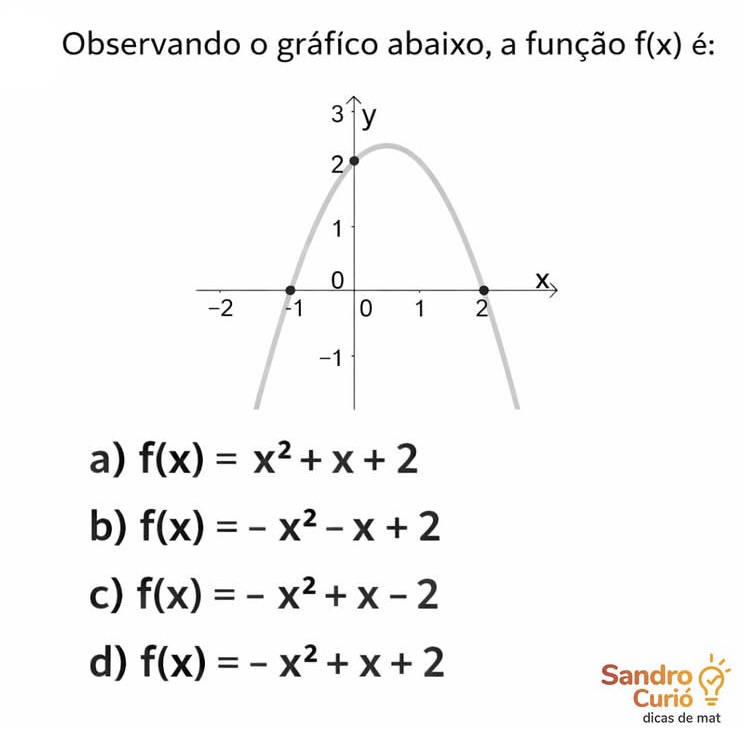
(Gráfico de uma parábola com concavidade para baixo, raízes em $x=-1$ e $x=2$, e intercepto $y$ em $y=2$.)

Opções:

a) $f(x) = x^2 + x + 2$

b) $f(x) = -x^2 – x + 2$

c) $f(x) = -x^2 + x – 2$

d) $f(x) = -x^2 + x + 2$

Análise e Resolução

A função apresentada no gráfico é uma função quadrática (ou função do segundo grau), cuja forma geral é $f(x) = ax^2 + bx + c$.

Passo 1: Análise da Concavidade (Coeficiente $a$)

•O gráfico é uma parábola com a concavidade voltada para baixo.

•Em uma função quadrática, a concavidade é determinada pelo coeficiente $a$:

•Se $a > 0$, a concavidade é para cima.

•Se $a < 0$, a concavidade é para baixo.

•Portanto, o coeficiente $a$ deve ser negativo ($a < 0$).

•Eliminamos a Opção (a), pois nela $a=1$ (positivo).

Passo 2: Análise do Intercepto $y$ (Coeficiente $c$)

•O ponto onde o gráfico intercepta o eixo $y$ é dado por $f(0)$, que é o valor do coeficiente $c$.

•Pelo gráfico, a parábola cruza o eixo $y$ no ponto $(0, 2)$.

•Portanto, $c = 2$.

•Eliminamos a Opção (c), pois nela $c=-2$.

Passo 3: Verificação das Raízes (Zeros da Função)

•As raízes da função são os pontos onde o gráfico intercepta o eixo $x$, ou seja, onde $f(x) = 0$.

•Pelo gráfico, as raízes são $x_1 = -1$ e $x_2 = 2$.

•Restam as opções (b) e (d). Vamos testar as raízes em ambas:

Opção	Função	Teste da Raiz $x=2$	Resultado
b	$f(x) = -x^2 – x + 2$	$f(2) = -(2)^2 – (2) + 2 = -4 – 2 + 2 = -4$	$f(2) \neq 0$. Incorreta.
d	$f(x) = -x^2 + x + 2$	$f(2) = -(2)^2 + (2) + 2 = -4 + 2 + 2 = 0$	$f(2) = 0$. Correta.

•Para confirmar, testamos a outra raiz na opção (d):f(-1) = -(-1)^2 + (-1) + 2 = -(1) – 1 + 2 = -2 + 2 = 0

•Ambas as raízes são satisfeitas pela função da Opção (d).

Resposta Correta

A função $f(x)$ é:

d) $f(x) = -x^2 + x + 2$

2. Sugestões de Questões para a Plataforma LMS

Para enriquecer o conteúdo do seu site exataseafins.shop e utilizar o potencial de uma plataforma LMS em WordPress, sugiro a criação de questões que abordem diferentes aspectos das funções quadráticas, focando em habilidades analíticas e de aplicação.

Tipo de Questão	Habilidade Focada	Exemplo de Enunciado
1. Determinação das Raízes	Cálculo das raízes (Fórmula de Bhaskara ou Soma e Produto)	Questão: Determine os zeros da função $f(x) = 2x^2 – 5x – 3$.
2. Coordenadas do Vértice	Cálculo do ponto de máximo/mínimo	Questão: O lucro $L$ de uma empresa é dado pela função $L(x) = -x^2 + 10x – 9$, onde $x$ é a quantidade de produtos vendidos. Qual é a quantidade de produtos que maximiza o lucro e qual é o lucro máximo?
3. Análise Gráfica e Coeficientes	Relação entre a função e seu gráfico	Questão: Uma função quadrática $f(x) = ax^2 + bx + c$ tem $a > 0$ e $c < 0$. Descreva a concavidade da parábola e a posição do seu intercepto $y$.
4. Análise do Discriminante ($\Delta$)	Determinação do número de raízes reais	Questão: Para qual valor de $k$ a função $f(x) = x^2 – 6x + k$ possui exatamente uma raiz real?
5. Reconstrução da Função	Uso de pontos notáveis para definir a função	Questão: Encontre a função quadrática $f(x)$ que possui vértice no ponto $(1, -4)$ e intercepta o eixo $y$ no ponto $(0, -3)$.

Sugestões de Formato para o LMS

Para o seu LMS, recomendo utilizar os seguintes formatos de questão para maximizar o engajamento e a avaliação:

1.Múltipla Escolha (MCQ): Ideal para as questões 1, 3 e 4. Permite correção automática e feedback imediato.

2.Resposta Numérica Curta: Ideal para as coordenadas do vértice (Questão 2) ou valores específicos (Questão 4).

3.Arrastar e Soltar (Gráfico): Se o seu plugin LMS suportar, crie questões onde o aluno deve arrastar a parábola para corresponder a uma função dada, ou vice-versa.

4.Resposta Aberta (Dissertativa): Para a Questão 5, onde o aluno deve inserir a função completa, permitindo uma avaliação mais aprofundada do raciocínio.

Essas sugestões garantem uma cobertura completa do tópico de funções quadráticas, desde o cálculo básico até a aplicação em problemas reais, alinhando-se perfeitamente com o foco do seu site exataseafins.shop.